Selection Sort
I am not good at this whole blogging thing anymore... My carpentry and remodeling skills have been put to the test over the last four months, however, as I've completely redone my kitchen and gutted and renovated my first-floor apartment. Now back into the saddle with some more algorithms!
Two posts ago, I started out with one of the fundamental sorting algorithms, Insertion Sort. Today we'll be looking at its close cousin, Selection Sort, which is described briefly in exercise 2.2-2 of CLRS.
If you recall, with Insertion Sort, we would iterate over our array taking the current value and then inserting it into the proper place in the elements that we have already sorted, by bubbling it down until the array left of our current position is sorted.
Selection Sort works slightly differently. Our algorithm, in English, is as follows:
-
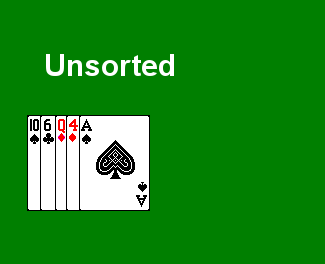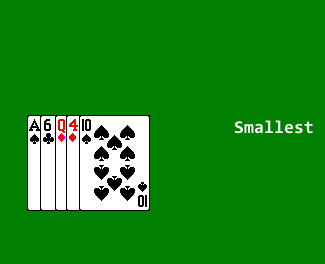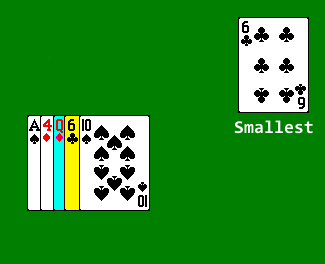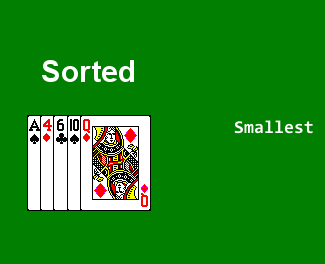
Scan through the array, to select the smallest value, and swap that value with the value in the first position.
-
Then scan through the rest of the array to find the next smallest value, and swap that value with the value in the second position.
-
Continue in this fashion until we reach the last element, at which point the array is sorted.
At first glance, this is very, very similar to Insertion Sort, but they are actually almost opposite. The key difference lies in the way that the comparisons are performed
-
In Insertion Sort, we select the next unsorted element, and scan backwards through the sorted elements to find the position that the current element should be placed.
-
In Selection Sort, we select the next position in the array, and scan forward through the remaining unsorted elements to find the element that should go in that position
This difference becomes important when we consider the best and worst case performance of the two algorithms.
-
For Insertion Sort, the best case is when we have an already sorted array and try to sort it again. In this case, we take each element, and need to only compare it against the preceding element, so that we have O(n) comparisons. The worst case is when we have a reverse sorted array, in which case, we will have to compare each new element against every previously sorted element, which gives us n(n-1)/2 comparisons, for a worst-case runtime of O(n2).
-
For Selection Sort, the best and worst case runtimes are the same. For every element, we have to scan all the remaining elements to find the smallest element, so that we must always perform n(n-1)/2 comparisons, so it is always O(n2).
-
One other difference between Insertion and Selection Sort is in the number of swaps that the two algorithms need to perform. Selection Sort will always perform O(n) swaps, whereas Insertion Sort can perform between 0, in the best case, to O(n2) swaps, due to the way it bubbles unsorted values into the sorted portion of the array.
Implementation
Now that I've done a few of these, I'm not going to go through all the different variations and C#-isms for generics and custom comparators, and just show the straightforward implementation for Selection Sort on an array of integers. If you want to see the full code, including a recursive version, it is available on GitHub.
public static void SelectionSort(this int[] a) {
for (var i = 0; i < a.Length-1; i++) {
var smallest = a[i];
var smallestI = i; // index of the smallest item
for (var j = i+1; j < a.Length; j++) {
if (a[j] < smallest) {
smallest = a[j];
smallestI = j;
}
}
// swap the smallest value into the final position
a[smallestI] = a[i];
a[i] = smallest;
}
}
Flying Spaghetti Monster willing, I'm done with renovation projects for a little bit, so I should have a little more time on my hands, and there won't be a multimonth layover before the next entry in this series, but you never know. Next up we'll be moving on to divide and conquer sorting algorithms, starting with Mergesort. Stay tuned.