An FPS Camera in SlimDX
Up until now, we have been using a fixed, orbiting camera to view our demo applications. This style of camera works adequately for our purposes, but for a real game project, you would probably want a more flexible type of camera implementation. Additionally, thus far we have been including our camera-specific code directly in our main application classes, which, again, works, but does not scale well to a real game application. Therefore, we will be splitting out our camera-related code out into a new class (Camera.cs) that we will add to our Core library. This example maps to the CameraDemo example from Chapter 14 of Frank Luna’s Introduction to 3D Game Programming with Direct3D 11.0 . The full code for this example can be downloaded from my GitHub repository, https://github.com/ericrrichards/dx11.git, under the CameraDemo project.
We will be implementing a traditional First-Person style camera, as one sees in many FPS’s and RPG games. Conceptually, we can think of this style of camera as consisting of a position in our 3D world, typically located as the position of the eyes of the player character, along with a vector frame-of-reference, which defines the direction the character is looking. In most cases, this camera is constrained to only rotate about its X and Y axes, thus we can pitch up and down, or yaw left and right. For some applications, such as a space or aircraft simulation, you would also want to support rotation on the Z (roll) axis. Our camera will support two degrees of motion; back and forward in the direction of our camera’s local Z (Look) axis, and left and right strafing along our local X (Right) axis. Depending on your game type, you might also want to implement methods to move the camera up and down on its local Y axis, for instance for jumping, or climbing ladders. For now, we are not going to implement any collision detection with our 3D objects; our camera will operate very similarly to the Half-Life or Quake camera when using the noclip cheat.
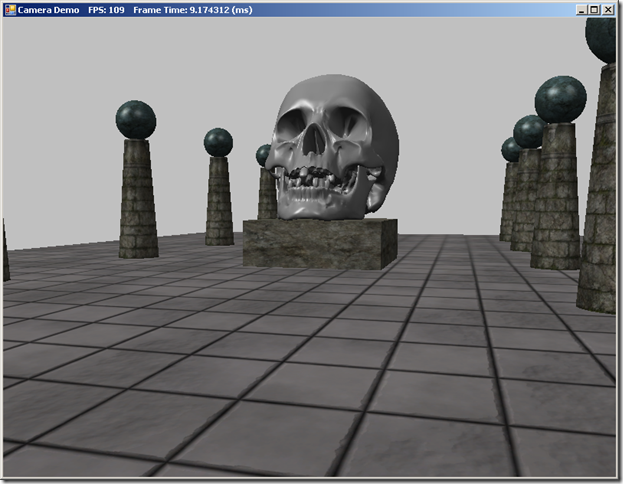
Our camera class will additionally manage its view and projection matrices, as well as storing information that we can use to extract the view frustum. Below is a screenshot of our scene rendered using the viewpoint of our Camera class (This scene is the same as our scene from the LitSkull Demo, with textures applied to the shapes).
The member properties of our Camera class are shown in the listing below:
public class Camera { public Vector3 Position { get; set; } public Vector3 Right { get; private set; } public Vector3 Up { get; private set; } public Vector3 Look { get; private set; } public float NearZ { get; private set; } public float FarZ { get; private set; } public float Aspect { get; private set; } public float FovY { get; private set; } public float FovX { get { var halfWidth = 0.5f * NearWindowWidth; return 2.0f * MathF.Atan(halfWidth / NearZ); } } public float NearWindowWidth { get { return Aspect * NearWindowHeight; }} public float NearWindowHeight { get; private set; } public float FarWindowWidth{ get { return Aspect * FarWindowHeight; }} public float FarWindowHeight { get; private set; } public Matrix View { get; private set; } public Matrix Proj { get; private set; } public Matrix ViewProj { get { return View * Proj; }} }
- Position, Right(X), Up(Y), Look(Z) – These vectors represent the position and orientation of our Camera’s local frame of reference. Only the Position property is exposed for editing by the user of the Camera class; the other three vectors are internally managed by the class, as we need to ensure that these vectors represent an orthonormal basis.
- NearZ, FarZ – These variables store the distance in view space to the near and far clipping planes of the Camera’s view frustum.
- Aspect, FovY, FovX – These properties control the field-of-view angle, in radians, of the camera, accounting for the aspect ratio of the rendering viewport.
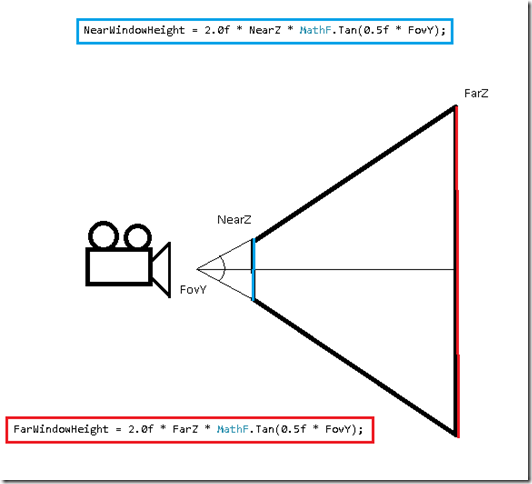
- NearWindowWidth, NearWindowHeight, FarWindowWidth, FarWindowHeight – These properties store the height/width dimensions of the near and far clipping planes in view space. Together with NearZ and FarZ, we can use these properties to calculate the the extents of the view frustum, which will come in handy when we come to the next chapter, and implement frustum culling.
- View, Proj and ViewProj – The Camera class manages its own view and projection matrices, which we will create helper functions to compute in a bit. The ViewProj property is provided for convenience, since we typically want to pass the combined matrix, rather than just the view or projection matrices, into our shaders.
Constructor
Our constructor for the Camera class is very simple. We setup the camera at the world origin, pointed down the Z axis. Then we use the SetLens() function ,which we will cover shortly, to create our projection matrix with a 45 degree field-of-view angle, an aspect ratio of 1, and our default near and far Z distances. Don’t be overly concerned with these values, as you will want to call SetLens on your application camera during the OnResize virtual function of your D3DApp-derived class, so that you can pass in the correct aspect ratio when the screen or viewport is resized.
public Camera() { Position = new Vector3(); Right = new Vector3(1, 0, 0); Up = new Vector3(0, 1, 0); Look = new Vector3(0, 0, 1); View = Matrix.Identity; Proj = Matrix.Identity; SetLens(0.25f * MathF.PI, 1.0f, 1.0f, 1000.0f); }
SetLens()
The SetLens() function computes the view frustum dimensions and creates the camera projection matrix, using the same Matrix.PerspectiveFovLH static function that we have been using in our previous examples.
public void SetLens(float fovY, float aspect, float zn, float zf) { FovY = fovY; Aspect = aspect; NearZ = zn; FarZ = zf; NearWindowHeight = 2.0f * NearZ * MathF.Tan(0.5f * FovY); FarWindowHeight = 2.0f * FarZ * MathF.Tan(0.5f * FovY); Proj = Matrix.PerspectiveFovLH(FovY, Aspect, NearZ, FarZ); }
A picture helps to visualize the geometry here:
LookAt()
We’ll provide a public method that allows you to set the camera and point it at something, which we’ll call LookAt(). We also need to pass in an up vector; in our usage, this will almost always be your standard (0,1,0) Y axis vector, but if you support rolling your camera on the Z axis, you’ll have need to pass in your current Up vector or a new computed Up vector. Essentially, what this function does is to recalculate our camera’s orthonormal basis.
public void LookAt(Vector3 pos, Vector3 target, Vector3 up) { Position = pos; Look = Vector3.Normalize(target - pos); Right = Vector3.Normalize(Vector3.Cross(up, Look)); Up = Vector3.Cross(Look, Right); }
UpdateViewMatrix()
Whenever the camera moves or rotates, we will need to recreate our view matrix. Typically, we will do this every frame, in our DrawScene method. We could use the SlimDX Matrix.LookAtLH(eye, target, up) function to create our view matrix, if we calculated the target point from our camera Look vector and our FarZ property. (At least, I think that that would work, though I haven’t experimented with it yet.) However, Mr. Luna illustrates how one would generate a view matrix based on the camera position and basis vectors, so that is the method I am following. First, we re-normalize our basis vectors, in case they have become non-orthonormal. Next, we fill out our new view matrix, using the derivation of the view-to-world space transform presented in Section 14.1, reproduced below, then set the new view matrix to our View property.
public void UpdateViewMatrix() { var r = Right; var u = Up; var l = Look; var p = Position; l = Vector3.Normalize(l); u = Vector3.Normalize(Vector3.Cross(l, r)); r = Vector3.Cross(u, l); var x = -Vector3.Dot(p, r); var y = -Vector3.Dot(p, u); var z = -Vector3.Dot(p, l); Right = r; Up = u; Look = l; var v = new Matrix(); v[0, 0] = Right.X; v[1, 0] = Right.Y; v[2, 0] = Right.Z; v[3, 0] = x; v[0, 1] = Up.X; v[1, 1] = Up.Y; v[2, 1] = Up.Z; v[3, 1] = y; v[0, 2] = Look.X; v[1, 2] = Look.Y; v[2, 2] = Look.Z; v[3, 2] = z; v[0, 3] = v[1, 3] = v[2, 3] = 0; v[3, 3] = 1; View = v; }
Camera Movement
We will provide helper methods to move our camera in the X & Z planes, and to rotate the camera about the Right and Up basis vectors. In the context of an FPS game, these actions are typically referred to as Walk, Strafe, Pitch and Yaw, respectively. We will constrain the Yaw function to only rotate about the Y axis, as the effect tends to look better that way.
public void Strafe(float d) { Position += Right * d; } public void Walk(float d) { Position += Look * d; } public void Pitch(float angle) { var r = Matrix.RotationAxis(Right, angle); Up = Vector3.TransformNormal(Up, r); Look = Vector3.TransformNormal(Look, r); } public void Yaw(float angle) { var r = Matrix.RotationY(angle); Right = Vector3.TransformNormal(Right, r); Up = Vector3.TransformNormal(Up, r); Look = Vector3.TransformNormal(Look, r); }
Using the Camera Class
In our demo application, we will replace our previous camera variables (_phi, _theta, _radius, _view, _proj), with an instance of our new Camera class. We construct the camera in our constructor, like so:
public CameraDemo(IntPtr hInstance) : base(hInstance) { // snip... _cam = new Camera(); _cam.Position = new Vector3(0, 2, -15); // snip... }
We must reconstruct the Camera’s projection matrix in our OnResize() function, by calling the Camera’s SetLens() method, like so:
public override void OnResize() { base.OnResize(); _cam.SetLens(0.25f*MathF.PI, AspectRatio, 1.0f, 1000.0f); }
To move our camera around the scene, we add the following code to our UpdateScene() method.
public override void UpdateScene(float dt) { base.UpdateScene(dt); if (Util.IsKeyDown(Keys.Up)){ _cam.Walk(10.0f*dt); } if (Util.IsKeyDown(Keys.Down)) { _cam.Walk(-10.0f * dt); } if (Util.IsKeyDown(Keys.Left)) { _cam.Strafe(-10.0f*dt); } if (Util.IsKeyDown(Keys.Right)) { _cam.Strafe(10.0f * dt); } }
Because we want to use the elapsed frame time to control the amount of movement, we cannot use our previous method of binding to the Form.KeyDown method to catch the keystrokes. For a more full-fledged example, we would probably want to write an input handling class, wrapping DirectInput, but for our purposes, we can just use the Windows API function GetAsyncKeyState(). The .Net framework does not provide (at least as far as I know…) a direct analog of this function; however, we can import the native Win32 library user32.dll (which contains GetAsyncKeyState()) using DllImport and writing a wrapper around the native function, which I have added to our Util class.
[DllImport("user32.dll")] static extern short GetAsyncKeyState(System.Windows.Forms.Keys vKey); public static bool IsKeyDown(System.Windows.Forms.Keys key) { return (GetAsyncKeyState(key) & 0x8000) != 0; }
We can pan our camera using the mouse by adding the following code to our OnMouseMove function:
protected override void OnMouseMove(object sender, MouseEventArgs e) { if (e.Button == MouseButtons.Left) { var dx = MathF.ToRadians(0.25f * (e.X - _lastMousePos.X)); var dy = MathF.ToRadians(0.25f * (e.Y - _lastMousePos.Y)); _cam.Pitch(dy); _cam.Yaw(dx); } _lastMousePos = e.Location; }
Lastly, when we draw our scene, we need to update the camera’s view matrix, and grab the view and projection matrices to be input to our shader variables.
public override void DrawScene() { // ...snip _cam.UpdateViewMatrix(); var view = _cam.View; var proj = _cam.Proj; var viewProj = _cam.ViewProj; // ..snip }
The CameraDemo application in action:
Next Time…
We’ll move on to Chapter 15, and take a look at view-frustum culling, to avoid drawing objects that will be clipped out of the viewing volume, and at hardware-instanced geometry, which will allow us to render multiple copies of the same geometry more efficiently.